Purdue University 2001 Swine Research Report

Nonlinear Mixed Effects Model for Swine Growth

A. P. Schinckel and B. A. Craig
Department of Animal Sciences and Department of Statistics, Purdue University

Introduction

Several nonlinear growth functions model weight as a function of days of age. Typically these functions are solved by iterative procedures that minimize the residual variance. The residual values (the observed minus predicted live weights) are assumed to be independent with a constant variance.

Growth curves are often fit to serial live weight data typically every 14-21 days from 50 lbs. to 250 lbs. live weight. This serial data usually has underlying relationships or correlations amongst the serial live weight observations. Heavier pigs at birth and weaning usually have a competitive advantage and remain heavier than the remaining pigs of the group. Also, the variation amongst the pigs for live weight increases as age increases. This typical result contradicts the assumption that the residual values are independent and are a constant variance at each age.

Also, marketing pigs in a specific live weight range or ending research trials at a specific live weight may bias the growth curves. To avoid discounts for pigs outside the specific pork processor’s optimal carcass weight ranges, the fastest growing pigs are marketed early and the slowest pigs are marketed later. By including live weight data after the fastest gaining pigs have been marketed, under predicts the true growth rates especially after 200 lbs. live weight (Schinckel and DeLange, 1996; Smith et al., 1999).

The objective of this study was to evaluate the use of a mixed effects version of a commonly used live weight growth curve.

Materials and Methods

Swine growth data was fit to the Bridge’s function, where WTGAIN_t is the expected live weight gain from birth to age t, C is mature weight, m is the exponential growth decay constant, a is the kinetic order constant, and e_it is the residual weight gain for the i^th pig at time t. The e_it are assumed to be normally distributed with mean zero and variance Var(e).

The mixed effects model 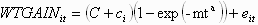is   where c_i is the random effect for the i^th pig. The c_i’s are assumed to be normally distributed with a mean of zero and variance Var(c). This model simply allows the mature weight C to vary amongst the pigs. The variance in live weight at a specific age is . The total variance at a specific age can be partitioned into the amount caused by the variation between pigs or (Var c/C²)(WTGAIN_t)² and the residual variance (Var(e), or variance of each pig’s live weights from their predicted values from the mixed model) is assumed to be constant. This model assumes a constant between pig coefficient of variation and predicted as [(Var (c))/C²]^1/2. The covariance of serial live weights at two ages (t = 1 and t = 2) can be expressed as = (Var (c)/C²) WTGAIN₁  * WTGAIN₂. These expressions account for the increasing variance in live weight as age increases and greater serial correlations at the later ages (greater live weights) than the early ages.

Data Analysis

To evaluate the improved fit of the mixed effects model, serial live weight data from 93 pigs taken at 54, 68, 82, 96, 110, 124, and 138 days of age were used. To demonstrate the mixed model’s decreased sensitivity to selective sampling, both the traditional fixed and mixed effects model were fit to a data set in which the heaviest 15% were removed after 110 days of age and the next heaviest pigs removed at 124 days of age.

The data was analyzed using NLINMIX procedures of SAS. Since the exponential growth decay parameter was close to zero, the model was re-parameterized where (m' = log(m)) to help with the convergence of the solution of the nonlinear regression parameters and approximate standard errors.

Results

Fixed Effects Model

The parameters estimates are summarized in Table 1. To demonstrate the violation of assumptions, Table 2 summarizes the covariances and correlations (observed minus predicted values) among the residuals at different ages. The residual variance increases over time (main diagonal) and the covariances among the sequential residuals increase as the age of the pig increases. The correlations have a distinct pattern. The correlations between residuals decrease as the time span between the observations increase. The correlations between subsequent observations (14 d apart or 28 d apart) are much larger at the later ages than early ages. This is due to the fact that the part-whole relationships between biweekly weights increase as live weight increases.

Mixed Effects Model

The between pig variability is modeled by varying the mature weight. This builds the observed increasing variance and covariance relationships with age directly into the model. The mixed model parameter estimates are also presented in Table 1. The estimates do not change due to the fact that the mean of the mixed effects model is the same as the fixed effects and all pigs were observed at each age. The overall variation has partitioned into the within pig variation (i.e., VAR e) and the between pig variation (i.e., VAR c). The approximate standard error for each parameter has been significantly reduced, almost halved. This improvement in precision is also apparent when estimating the growth rate at each age. These estimates and standard errors are presented in Table 3. The difference in standard errors is most noticeable at the older ages as the between pig variation increases.

Selective Sampling

Another important feature of the mixed effects model is its ability to handle the potential bias that comes with the early removal of heavier pigs. To demonstrate this, the heaviest 15% (14 pigs) is removed after d 110 and again after d 124 (12 pigs). Both the fixed and mixed model parameter estimates are summarized in Table 4. The mature weight shifted substantially downward using the fixed model but only slightly in the mixed effects model. In the mixed model, because the weights of each pig vary about a pig-specific growth curve, the selective sampling does not have a large effect on the average population curve.

Discussion

Accurately characterizing the growth potential for a population of pigs is necessary to identify alternative strategies to improve the efficiency and daily nutrients required for swine production. It was shown for these pig, data that simply allowing the mature weight parameter to vary, provided an adequate explanation for the increasing variance and serial correlation, and thus fit the data much better than the fixed effects model.

Recently, pork producers have become concerned with quantifying and reducing variation in the growth of pigs (Schinckel et al., 1998; Smith et al., 1999). This version of a mixed model produces an increasing variance, a decreasing coefficient of variation, and increasing serial correlations amongst sequential live weights as age increases. These changes in parameters are commonly found in pig growth data (King, 1999; Smith et al., 1999). Stochastic modeling is also straightforward within the mixed effects version since only one additional variable (c_i) needs to be simulated to model the growth of each pig.

With fixed effects models, any removal of the fast-gaining pigs at marketing or live weight in research trials biases the growth curves. In the past, one option has been to only include data prior to the marketing of any animals (Smith et al., 1999). Producers could purposely not remove pigs, however that could create a greater effective stocking density than their normal sequential marketing procedures. The use of the live weight data only up to a mean weight of 240 lbs. resulted in large bootstrap standard errors for the predicted growth rates from 210-240 lbs. live weight (Schinckel et al., 1998). The use of a mixed effects model allows the marketing of animals sequentially at their ideal market weight range, as normally would be done, and include all the live weight data without severely biasing the predicted growth curve parameters.

It may be important to note that the mixed model uses a maximum likelihood solution versus some nonlinear solutions that utilized minimum least-squares. The parameters C, Var(c), and VAR e are the set of values which best describe the relative magnitude of the between pig and within pig variation. If the correlations between the serial live weights are high, indicating that the heaviest pigs stay heavier and light pigs lighter, then the ratio of [Var(c_i)/(C²] to Var e will be high. This also implies that the use of the individual c_i produces a growth curve with only small deviations from the pig’s individual growth curve. The larger the absolute and relative magnitude of the Var e, the lower the correlations amongst the serial live weights and greater the deviations of each pig’s live weights from it’s individual curve using the c_i for that specific pig. These statistics may be used to parameterize both the amount and type of between pig and within pig variation that produces the total amount of variation in live weight at any specific age.

Implications

Animal growth models have been developed with a goal of optimizing production systems. These models require a parameterization of animal growth. Nonlinear mixed effects models allow a more precise evaluation of animal growth functions than the traditional fixed effects models. Mixed effects models can also reduce the impact of potential biases of selective sampling and provide an additional parameter that describes animal to animal variation.

References

King, R. H. 1999. A Review - Nutritional constraints to pig performance and pig variability. Manipulating Pig Production VII. Agriculture Victoria, Victorian Institute of Animal Science, Private Bag 7, Werribee, Vic. 3030. pp. 245-251.

Schinckel, A. P. and C. F. M. deLange. 1996. Characterization of growth parameters needed as inputs for pig growth models. J. Anim. Sci. 74:2021-2036.

Schinckel, A. P., J. W. Smith, M. D. Tokach, M. E. Einstein, J. L. Nielsen, and R. D. Goodband. 1998. Sampling errors associated with protein accretion and amino acids requirements predicted from serial live weight and real-time ultrasound measurements. 1998 Purdue Swine Day. West Lafayette, IN 47907. pp. 175-184.

Smith, J. W., M. D. Tokach, A. P. Schinckel, S. S. Dritz, M. Einstein, J. L. Nelssen, R. D. Goodband. 1999. Developing farm-specific lysine requirements using accretion curves: Data collection procedures and techniques. Swine Health Prod. 7(6):277-282.

Table 1. Parameter Estimates and Approximate Standard Errors for Bridges’ Model^a based on serial growth data (54, 68, 82, 96, 110, 124, and 136 d) from 93 pigs

The fixed effects version is live weight gain (kg) from birth equals where e is Normal with variance s². The mixed effects model is , where e is Normal with variance Var (e) and c_i, the i^th pig’s random effect, is Normal with variance Var (c)

Table 2. Variances, covariances and correlations of the residuals (lb² fixed model, N=93)^a

^a Variances on the diagonal, covariances (COV) and correlations (r) on the off diagonal

Table 3. Rate of growth ADG (lb/d), estimates and standard errors^a

^aEstimate based on fixed effects model

Table 4. Parameter estimates under serial marketing^a

^aThe fixed effects version is live weight gain (lb) from birth equals , where e is Normal with variance Var (e). The mixed effects model is , where e is Normal with variance Var (e) and c_i, the i^th pig’s random effect, is Normal with variance Var (c)

Index of 2001 Purdue Swine Research Articles