Purdue University 2002 Swine Research Report

Alternative Nonlinear Mixed Effects Models for Swine Growth

A. P. Schinckel¹, M. E. Einstein¹, and B. A. Craig²
Departments of ¹Animal Sciences and ²Statistics

Introduction

The production of pigs has developed towards highly specialized coordinated production systems. Variability in the growth rates of pigs is important to the economic costs and returns of both the pork producer and processor. The optimization of pork production systems including the evaluation of alternative management and marketing strategies requires knowledge of the variation in body weight and carcass composition.

Typically, pigs are weighed every 14-21 days from 50 lbs to 250 lbs live weight to develop live weight growth curves. Heavier pigs at weaning usually have a competitive advantage and remain heavier than the other pigs of the group, all the way to market. Also, the variation among the pigs for live weight increases as age increases. The objective of this study was to evaluate alternative mixed effects models of a standard growth function.

Materials and Methods

Swine Growth Model. Consider the following fixed effects growth model,

WTGAIN_i,t = WT_i,t - WT_i,0 = C(1-exp(-Mt^A)) + e_i,t ,

proposed by Bridges. Here WTGAIN_i,t is the weight gain from birth to age t, WT_i,t is the weight at age t, t is the days of age, C is the average mature body weight, M is the exponential growth decay constant and A is the kinetic order constant. Typically, a constant value of 3.1 lb is used for birth weight (WT_i,0). Since the exponential decay parameter is close to zero, the model was reparamaterized (M' = ln(M)) with the form WTGAIN_i,t = C ((1-exp(-exp (M') t^A)).

In this function, any combination of C, M', or A could be included as random effects. For example, the mixed model with all three random effects can be expressed as WTGAIN_i,t = (C + c_i)(1 – exp (-exp(M' + m'_i) t^{(A + a_i)} + e_i,t , where c_i, m'_i and a_i would be each pig’s random effects assumed to be multivariate normal with mean 0 and variances s_c², s_m'², and s_a², respectively. Additionally, the random effects of each pig may be correlated.

The simplest single random effects model has the form WTGAIN_i,t = (C + c_i)(1 – exp (-exp(M') t^A) + e_i,t , where c_i is the random effect for each pig . This mixed effects growth function can also be written as WTGAIN = (C + c_i) f(t) , where f(t) = [1 - exp (-exp(M') t^A)] which increases from 0 (when t = 0) to an upper limit of one. In this form, the total variance of WTGAIN_i,t, at time t, can be separated into the between pig variance, s_c² [f(t)]², and within pig variance, s_e².

The inclusion of a second random effect (m'_i or a_i) accounts for different patterns of growth between pigs. The addition of m'_i or a_i as random effects with the c_i effects allows increased flexibility in fitting of the between pig variance. However, the formulas for the approximate between pig variances are more complicated.

Example data. The data are from a trial in which gilts were randomly assigned to be reared from 49 d of age in either a grow-finish facility that had been completely emptied, cleaned and disinfected (all-in, all-out management, AIAO) or a continuous-flow grow-finish facility (CF). A total of 96 AIAO gilts were weighed at 49, 70, 104, 132, and 153 d of age. Also, 42 AIAO gilts had an additional weight measured at 174 d of age. A total of 96 CF gilts were weighed at 49, 70, 104, 132, 153, and 174 days of age.

Estimation. The live weight data from each group of pigs were fitted to the reparameterized fixed effects Bridges function using the non-linear mixed (NLMIXED) procedure of SAS. The additional random effects were added in a step-wise order based on Akaike’s Information Criteria (AIC) values.

The NLMIXED procedure provided predicted values for the random effect of each pig, variance estimates for each random effect, residual variance, and the estimated covariance between the random effects. Approximate standard errors of the function parameters, variance estimates and covariance estimates were provided.

Results

The AIAO and CF gilts had similar mean weights up to 104 d of age. After 104 d of age, the growth rate of the CF gilts decreased to a greater extent than the growth rate of AIAO gilts, which decreased only a small amount (Table 1). The parameter estimates and nonlinear regression statistics are presented in Table 2. The R² and residual standard deviation (RSD) values were similar for the fixed effects functions for both groups of pigs. In each environment, the addition of a random effect c_i for each pig provided the best single random effect equation. For the AIAO pigs, the value of C increased from 327.8 to 496.4 lb. Of the 96 pigs, 54 were removed at 153 d of age upon reaching a target weight of 245 lbs, and 42 remained to 174 d of age. This caused a downward bias in the magnitude of C in the fixed effects model. The mixed effects model almost entirely decreases the magnitude of such bias produced by the early removal of pigs (Schinckel and Craig, 2001). The VAR(e) and RSD values were reduced and likelihood statistics improved with the addition of the c_i random effect. The approximate standard errors of M' and A were reduced for the single random effect versus the fixed effects equation.

The addition of a second random effect for m'_i had a relatively lesser impact to reduce the residual variance and improve the likelihood statistics. The significance of the m'_i random effect indicates pig-to-pig variation in the shape of the live weight growth curves. The random effect m'_i was negatively correlated with the random effect c_i (r = -0.82 and -0.76 for the AIAO and CF pigs). This correlation indicates that pigs with greater values of c_i had lower values of m'_i.

The SAS algorithms were not able to solve all three parameters as random effects. A form of multicolinearity existed between a_i and c_i. The multicolinearity was expressed through the equations F = 1 - e^(1/A-1) and F = BWMAX / C, where F is the fraction of mature weight at which maximum growth rate is achieved, BWMAX is the body weight where the maximum growth rate occurs and C is the mature body weight.

The nonlinear models can be used to predict the age required for each pig to reach a specific target body weight (BW). Using the two parameter mixed model and 3.1 lb as the initial BW, the age at a specific target body weight (TBW) for pig i is t_i = [(ln (1 – (TBW – 3.1)) / (C + c_i)) / (-exp (M' + m'_i))]1/a. The mean and variance of the predicted t_i can then be investigated under the different rearing programs. The difference in the predicted days required to reach TBW increased between the AIAO and CF pigs as TBW increased from 220 to 286 lb. The variability in the predicted age to reach a TBW increased as the TBW increased and the variability increased more rapidly for the CF gilts than the AIAO gilts.

The increased standard deviation of the CF gilts compared to the AIAO gilts is partially caused by the decreasing average daily gain of CF gilts after 104 d of age. The reduced growth of the CF pigs after 104 d of age compared to the AIAO gilts makes it more difficult to achieve a target weight of 264.5 lb in the CF environment than the AIAO environment.

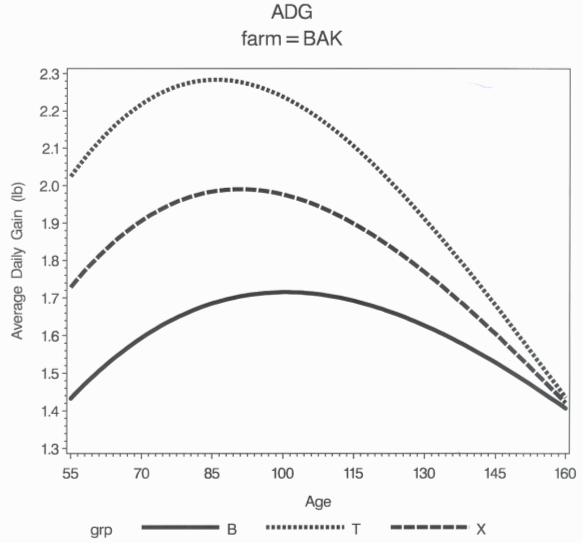
The random effects can be used to evaluate the growth of individual pigs or specific groups of pigs. The difference in the growth rates of the five fastest and five slowest gaining CF gilts based on the predicted age to reach 264.5 lb are shown in Figures 1 and 2. The fastest gaining CF gilts had greater average daily gain than average and five slowest growing gilts at all liveweights. The difference in growth rate between the five fastest and five slowest growing gilts primarily occurred before 104 days of age. After 104 days of age, the difference in average daily gain decreased.

The days of age to reach specific target weights was predicted for the five fastest gaining and five slowest gaining gilts to each environment based on the predicted age required to reach 264.5 lb (Table 3). The difference in age required to achieve 220 lb between the five fastest and five slowest growing gilts was similar for the two environments (38.8 and 36.6 days for the AIAO and CF pigs). The difference in age predicted to achieve 264.5 lb between the fastest and slowest growing gilts increased to 61 d in the CF environment and 53 d in the SEW environment.

Discussion

As the environmental conditions worsened, the CF gilts had more variable growth rates. This increased variation in days required to achieve specific market weights has an economic cost as most pork processors discount pigs below their specified target market weight. The economic evaluation of rearing pigs under AIAO or CF management must include both the impact of the differences in the mean performance and differences in the variation in growth.

Implications

To optimize pork production systems, swine management and marketing strategies must be refined. This requires accurate estimates of both the between pig and within pig sources of variation. Mixed model nonlinear regression analyses produce the parameters and variance-covariance estimates needed to reproduce the increasing variance and increasing serial correlations among the serial live weights as age increases.

References

Schinckel, A. P. and B. A. Craig. 2001. Nonlinear mixed effects model for swine growth. 2001 Purdue Swine Research Reports. pp 20-25.

Table 1. Means and standard deviations for liveweight, lb

Table 2. Parameter estimates and approximate standard errors for the Bridges Function

¹ The fixed effects version is weight gain from birth equals C(1 - exp(-exp(M') t^A)) + e , where e is Normal with variance s_e². The mixed effects model is (C + c_i) (1 - exp(-exp(M') t^A)) + e , where e is Normal with variance s_e² and c_i, the i^th pig’s random effect, is Normal with variance s_c². The mixed effects model with c and m' as random effects is (C + c_i) [1 – exp (-exp (M' + m'_i) t^A)] + e where e is Normal with variance s_e² and c_i and m'_i are the i^th pig's random effects with means 0 and variances s_c² and s_m², and with covariance of c with m s_c,m.

Table 3. Overall means and means for the fastest and slowest growing pigs^a with standard deviations for predicted age to achieve specific body weight^b

^a The five gilts with the least and greatest predicted days to achieve 264.5 lb live weight in each environment.
^b Using Bridges mixed model equation WT_i,t = (C + c_i) [- exp (-exp (M' + m'_i) t^A)] + 3.1; t_i,TBW = [(ln (1 - (TBW - 3.1)) / (C + c_i)) / (- exp (M' + m'_i))]^1/A, where C, M' and A are mean parameter values and c_i and m'_i are parameters for the i^th pig.

Figure 1. Average daily gain of gilts from 55 to 160 days of age. (B = lower 5%; T = upper 5%; X = mean based on predicted days to 265 lb)

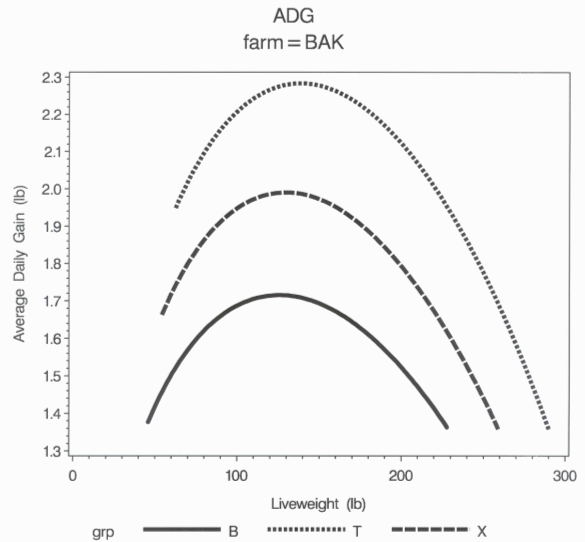
Figure 2. Average daily gain of gilts as related to liveweight. (B = lower 5%; T = upper 5%; X = mean based on predicted days to 265 lb)

Index of 2002 Purdue Swine Research Articles